Sound Waves
So what is sound, anyway? When you strike a tuning fork, you
hear a clear sound. That’s because striking the object
causes it to vibrate in a fairly simple back-and-forth manner,
but so quickly that you can’t really see the vibrations.
When a tine (prong) of the tuning fork moves away from its
resting position and impacts nearby air particles, it causes the
particles to scrunch together, creating a more dense area
(higher air pressure). This action is called compression.
When the tine then moves back past its resting position, the air
particles relax and spread out, creating a region of air less
dense (lower air pressure) than it was before you struck the
fork. This is called rarefaction. As the tine continues
to move back and forth, this causes a chain reaction, resulting
in areas of higher and lower air pressure propagating away from
the tuning fork as a sound pressure wave.
Imagine that you have a cylinder with a piston at one end
— rather like the cylinder in a car engine. The piston
moves back and forth, alternately compressing and rarefying the
air. If you were able to see the individual particles of air,
you would see higher pressure regions moving away from the
piston, as in the animation below.

Animation adapted from
Sound Waves, Institute of Sound and
Vibration Research (ISVR), University of Southampton, UK
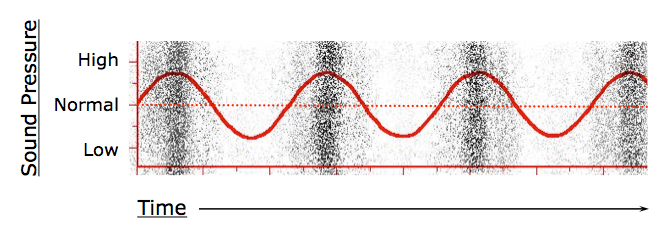
The piston is the large red object at the left; the tiny black
dots are air particles. The darker areas among the particles are
more dense — have higher pressure — than the
surrounding air. The three red dots mark individual air
particles. This shows that the air particles themselves do not
move very far as the wave passes through. Instead, they bob back
and forth, rather like a styrofoam cup thrown into gentle waves
in the ocean. (Don’t try this at the beach!) It’s
the pressure chain reaction — the acoustic energy of the
wave — that moves from one end of the cylinder to the
other.
In free air, a sound wave doesn’t just move in one
direction. It propagates in all directions. The picture below
shows what might happen to the surrounding air if you were to
ring a bell, assuming that there aren’t objects around
that partially block the propagation of the sound wave.

This is not a complete picture, though, because sound waves
propagate in three dimensions, not two — in a sphere, with
the sound source (the bell) in the center. The picture does
indicate that the difference in pressure between the compressed
and rarefied regions of air is more extreme closer to the sound
source. Sound waves lose energy due to air friction the further
away they propagate from the source.