When converting an analog audio signal to a digital representation, an AD converter takes amplitude measurements, or samples, of the waveform at equally spaced points in time. The sampling rate — i.e., the frequency of these measurements — determines the highest frequency of the input signal that can be captured. We saw in class that an insufficiently high sampling rate causes the loss of high frequencies, resulting in muted or murky sound quality. (For a review of these ideas, see Digital Audio, Part 1.)
Introduction to Digital Audio, Part 2
Sampling Resolution
Sampling resolution refers to the accuracy, rather than the frequency, of these amplitude measurements. The greater the accuracy, the more faithful is the digital representation of an analog audio signal. Accuracy depends on the kind of numbers used to encode the amplitude measurements. Most converters use integers to store these measurements.
Consider the waveform graph of an analog signal shown below.
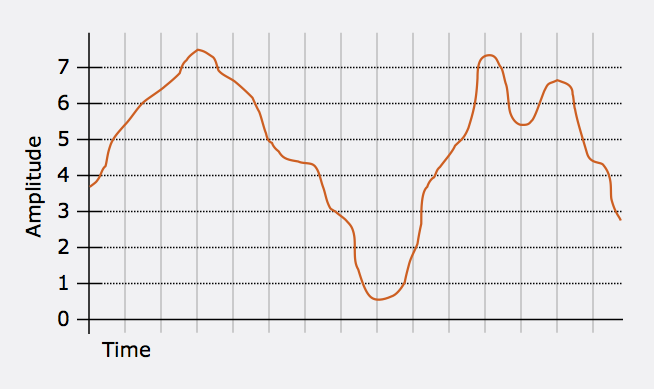
The gray vertical lines indicate moments when we take a measurement of the amplitude of the analog signal, governed by the sampling rate. The gray horizontal lines are the integer values that are available for representing those measurements. In this example, there are only eight integers. When we take a measurement, we need to round off the real value of the analog waveform to the nearest integer. This process is called quantization.
The blue stars below are the integer measurements. The resulting series of integers is 5 6 7 7 5 4 3 1 2 5 7 5 7 4, which is the stream of numbers that the computer stores to represent this waveform.

Quantization Error
Some of these measurements are very close to the waveform values, while others are not. For example, measurement A below is exactly right. However, measurement B requires a significant amount of round-off when we approximate the real analog value to the nearest integer.
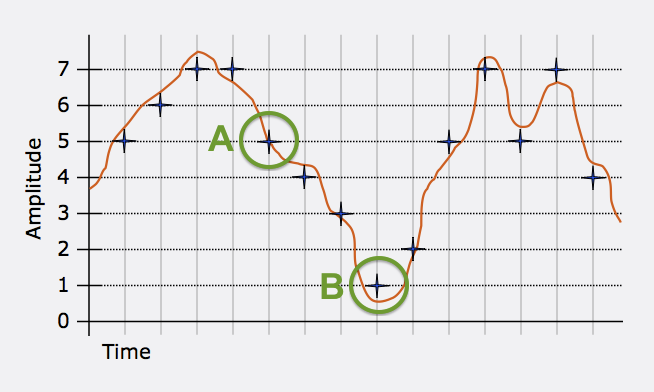
The amount of round-off is called quantization error. It tends to be randomly distributed for audio signals of any complexity, so if you graph the amount of error for a stream of audio samples, you’ll get a series of random numbers. The quantization error for each measurement is graphed at the bottom of the illustration below.
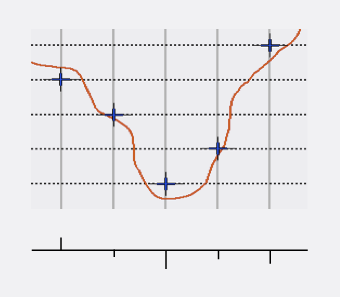
In a digital system, when you play back random numbers as an audio signal, you get noise. This noise is added to the desired part of the signal. So, too much quantization error produces a noisy audio signal. For this reason, quantization error is also known as quantization noise.
Increasing Sampling Resolution
To combat quantization noise, you merely need to increase the number of values that an integer can assume. In a digital system, integers are represented by groups of binary digits, or bits. The more bits you allocate to an integer, the greater the number of values that integer can have.
The following formula tells us exactly how the number of values an integer can have depends on the number of bits available to represent the integer.
number of values = 2N
(where N is the number of bits)
So 3 bits gives us 8 possible values, from 0 to 7, while 4 bits gives us 16 values, from 0 to 15. (If you want to confirm this, click the More about Binary Numbers button on page 1 of the MIDI app.)
Notice that adding just a single bit doubles the number of values available. In the previous example, we used 3-bit quantization, with values from 0 to 7. Now we add one bit to perform 4-bit quantization. This gives us an additional horizontal integer line between every pair of lines in the previous example, doubling the resolution.
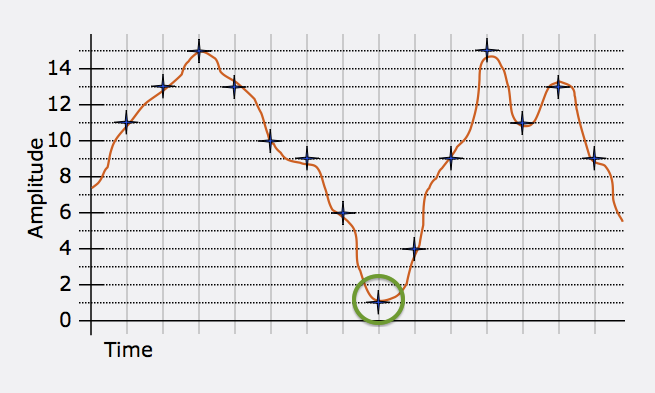
Now the circled measurement requires hardly any rounding off. Compare with the 3-bit case, shown again below.

The number of bits used to form an integer is known as the bit depth or word length. In the early days of samplers (mid-1980’s), it was common to use 8-bit samples. While that is much better resolution than our 4-bit sampling system above, it is far worse than the 16-bit samples used in CDs. In fact, adding 8 bits to each integer gives you a resolution that is 256 times greater. So in a 16-bit system, you get 256 additional integer grid lines between each pair of lines in an 8-bit system.
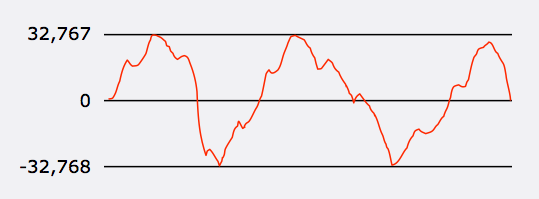
Using 16-bit integers gives you 65,536 distinct values. These are normally positioned symmetrically around zero, because that is the value that represents ambient air pressure, or zero amplitude. So the range of values for 16-bit samples is between -32,768 and 32,767.
Clipping
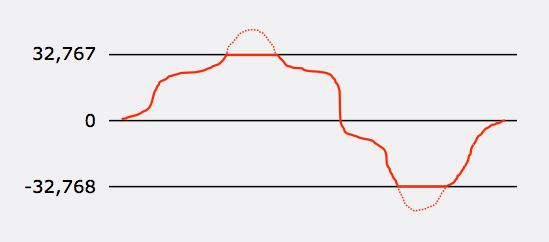
What happens if the real analog amplitude value you want to represent requires an integer value greater than 32,767? Tough luck — there’s no way to represent a value greater than that with 16 bits, so the value will be truncated to 32,767. (The same thing happens on the negative end, with values that are less than -32,768.) This is called clipping, which produces distortion that can be severe if prolonged. The following illustration shows two places where the analog waveform exceeds the range of a 16-bit integer (the dotted segments of the curve), resulting in a clipped waveform (the flat segments at 32,767 and -32,768) after conversion to digital.
The sound files we use every day in computer music software typically have word lengths of 16 and 24 bits. 24-bit audio has 256 times the resolution of 16-bit audio. This is especially useful when you work with sound that has very low amplitude, such as at the ends of long piano decays or reverberation tails. Even when the signal gets close to zero, there will still be sufficient resolution to represent it accurately without adding too much quantization noise.
| Bit depth | Usage |
|---|---|
| 8-bit integer | Historical interest only |
| 16-bit integer | CD, consumer audio |
| 24-bit integer | Professional audio |
| 32 or 64-bit floating point (not integer) | Internal representation in software |
Uncompressed Audio Data Rate
Uncompressed digital audio, described above, gives you very high quality. But it may require too much network bandwidth to transmit over slower Internet or cell phone connections. That’s where the familiar MP3 format comes in.
Consider the example of CD audio, which uses 16-bit samples at a 44,100 Hz sampling rate. There are two parallel streams, one for each channel, to produce stereo. What is the transmission rate of CD-quality audio?
As long as you understand the terms involved, this is a straightforward math problem. For each of the two channels, there are 44,100 samples per second. Each of these samples requires 16 bits. Transmission rates are normally described in terms of the number of bits per second that must flow from the source to the destination. In our case:
44100 samples per second
* 16 bits per sample
* 2 channels
= 1411.2 kbps
(where kbps is “kilobits per second,” or thousands
of bits per second)
This works out to about 10 MB (megabytes) per minute.
Lossy Compression of Audio: MP3 and AAC
The MP3 format was invented in the mid-1990’s to reduce the data transmission and storage demands of uncompressed audio. The kind of compression used to reduce the size of word processing files, such as ZIP, is not very effective for audio. Instead, MP3 uses perceptual coding to minimize the amount of data required to transmit and store audio. This takes advantage of psychoacoustic principles such as masking, in which, for example, loud sounds make it hard to hear soft sounds that are close in frequency. Instead of having a fixed number of bits per sample, as in uncompressed audio, an MP3 compressor allocates bits flexibly to different portions of the sound. Parts of the sound stream that require greater resolution get more bits. Parts that might be masked in our hearing get fewer bits. By being stingy with bits in this way, a compressor can save a lot of storage space. There are different data rates available for MP3 files, depending on the quality you want (e.g., 128 kbps, 160 kbps, 192 kbps, 256 kbps, etc.). These are anywhere from 5 to 11 times smaller than uncompressed audio.
The catch is that MP3 is a lossy format. Although it is based on sophisticated assumptions about how human hearing works, the bit allocation mentioned above discards information. When you turn an MP3 file into uncompressed audio, such as when you play it, some of the original sound data is gone forever. MP3 does a good job, but people who are very sensitive to audio quality, and are listening on professional equipment, can hear the artifacts of compression.
The AAC format (.m4v) is a more recent lossy format that achieves better sound quality than MP3 for the same amount of storage space. AAC is one of the formats available within Apple Music.

